Пример обработки статистического ряда абсолютных частот нашим сервисом:
(полигоны частот, гистограмма, функция распределения, математическое ожидание, дисперсия)
Задача:
Задан группированный статистический ряд абсолютных частот:
| xk* | 0.09073 | 0.27118 | 0.45163 | 0.63208 | 0.81253 | 0.99298 | 1.17343 | nk* | 76 | 51 | 39 | 36 | 21 | 18 | 9 |
| xk* | 1.35388 | 1.53433 | 1.71478 | 1.89523 | 2.07568 | 2.25613 | 2.43658 | nk* | 7 | 6 | 6 | 4 | 2 | 0 | 1 |
| xk* | 2.61703 | 2.79748 | 2.97793 | 3.15838 | 3.33883 | 3.51928 | 3.69973 | nk* | 0 | 1 | 1 | 0 | 0 | 0 | 2 |
Требуется построить (вычислить):
- группированный статистический ряд относительных частот из 21 члена(ов);
- полигон абсолютных частот;
- полигон относительных частот;
- гистограмму относительных частот;
- эмпирическую функцию распределения;
- выборочное среднее (Оценку математического ожидания);
- выборочную дисперсию (Оценку дисперсии);
РЕШЕНИЕ:
1. Строим группированный статистический ряд относительных частот.
Группированным статистическим рядом относительных частот называется последовательность пар чисел(x1* , n1*/n) , (x2* , n2*/n) ,…, (xm* , nm*/n)
где nk*/n — относительные частоты и n - объем выборки.
1.1. По группированному статистическому ряду абсолютных частот находим объем выборки n, просто суммируя абсолютные частоты:
76+51+ ... +2 = 280
1.2. Вычисляем относительные частоты nk*/n, как отношения абсолютных частот к объему выборки. результат представим в виде таблицы:
| Номер Интервала k | Центр Интервала xk* | nk* | nk*/n |
| 1 | 0.09073 | 76 | 0.27143 |
| 2 | 0.27118 | 51 | 0.18214 |
| 3 | 0.45163 | 39 | 0.13929 |
| 4 | 0.63208 | 36 | 0.12857 |
| 5 | 0.81253 | 21 | 0.07500 |
| 6 | 0.99298 | 18 | 0.06429 |
| 7 | 1.17343 | 9 | 0.03214 |
| 8 | 1.35388 | 7 | 0.02500 |
| 9 | 1.53433 | 6 | 0.02143 |
| 10 | 1.71478 | 6 | 0.02143 |
| 11 | 1.89523 | 4 | 0.01429 |
| 12 | 2.07568 | 2 | 0.00714 |
| 13 | 2.25613 | 0 | 0.00000 |
| 14 | 2.43658 | 1 | 0.00357 |
| 15 | 2.61703 | 0 | 0.00000 |
| 16 | 2.79748 | 1 | 0.00357 |
| 17 | 2.97793 | 1 | 0.00357 |
| 18 | 3.15838 | 0 | 0.00000 |
| 19 | 3.33883 | 0 | 0.00000 |
| 20 | 3.51928 | 0 | 0.00000 |
| 21 | 3.69973 | 2 | 0.00714 |
1.3. Убеждаемся, что сумма всех относительных частот nk*/n равна единице. (допускается небольшое отличие от единицы в рамках погрешности вычислений)
0.27143+ 0.18214+ ... + 0.00714 = 1.00000
ОТВЕТ. Группированный статистический ряд относительных частот имеет вид:
| xk* | 0.09073 | 0.27118 | 0.45163 | 0.63208 | 0.81253 | 0.99298 | 1.17343 | nk*/n | 0.27143 | 0.18214 | 0.13929 | 0.12857 | 0.07500 | 0.06429 | 0.03214 |
| xk* | 1.35388 | 1.53433 | 1.71478 | 1.89523 | 2.07568 | 2.25613 | 2.43658 | nk*/n | 0.02500 | 0.02143 | 0.02143 | 0.01429 | 0.00714 | 0.00000 | 0.00357 |
| xk* | 2.61703 | 2.79748 | 2.97793 | 3.15838 | 3.33883 | 3.51928 | 3.69973 | nk*/n | 0.00000 | 0.00357 | 0.00357 | 0.00000 | 0.00000 | 0.00000 | 0.00714 |
2. Строим полигон абсолютных частот.
Полигон абсолютных частот группированного статистического ряда абсолютных частот — это ломаная с вершинами в точках (xk* , nk* ). Полигон является одним из графических представлений выборки. Следует тщательно выбрать масштабы и начальные точки на осях, чтобы полигон был максимально наглядным.2.1. На оси абсцисс выбираем начальную точку чуть левее точки x1* = 0.09073, и такой масштаб, чтобы на оси поместился интервал [x1* , x21* ] = [ 0.09073 , 3.69973] и отчетливо различались точки xk*.
2.2. На оси ординат выбираем начало отсчета в точке 0 и такой масштаб, чтобы на оси поместился интервал
[min{n1*,…,n21* },max{n1*,…,n21* }] = [0 , 76] и отчетливо различались точки nk*.
2.3. На оси абсцисс размещаем значения xk*, а на оси ординат значения nk*.
2.4. Наносим точки (x1*, n1* ), (x2*, n2* ),…,(x21*, n21* ) на координатную плоскость и последовательно соединяем их отрезками. Получаем полигон, изображенный на рисунке ниже.
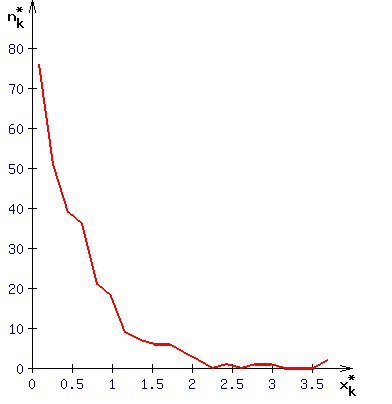
3. Строим полигон относительных частот.
Полигон относительных частот группированного статистического ряда относительных частот — это ломаная с вершинами в точках (xk* , nk*/n ). Полигон является одним из графических представлений выборки. Следует тщательно выбрать масштабы и начальные точки на осях, чтобы полигон был максимально наглядным.3.1. На оси абсцисс выбираем начальную точку чуть левее точки x1* = 0.09073, и такой масштаб, чтобы на оси поместился интервал [x1* , x21* ] = [ 0.09073 , 3.69973] и отчетливо различались точки xk*.
3.2. На оси ординат выбираем начало отсчета в точке 0 и такой масштаб, чтобы на оси поместился интервал
[min{n1*/n,…,n21*/n},max{n1*/n,…,n21*/n}] = [ 0.00000 , 0.27143] и отчетливо различались точки nk*/n.
3.3. На оси абсцисс размещаем значения xk*, а на оси ординат значения nk*/n.
3.4. Наносим точки (x1*, n1*/n ), (x2*, n2*/n ),…,(x21*, n21*/n ) на координатную плоскость и последовательно соединяем их отрезками. Получаем полигон, изображенный на рисунке ниже.
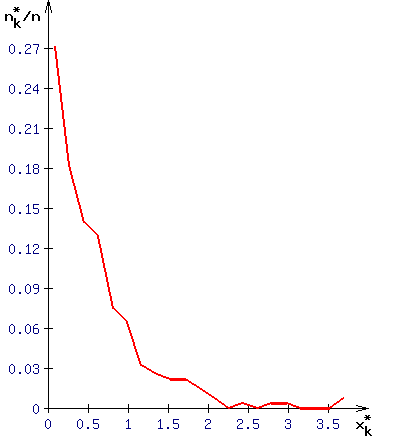
4. Строим гистограмму относительных частот.
Гистограмма относительных частот — это фигура, состоящая из m прямоугольников, опирающихся на интервалы группировки. Площадь к-ro прямоугольника полагают равной nk*/n, т.е. относительной частоте данного интервала.Для построения гистограммы нам необходимо получить границы интервалов группировки, для этого:
4.1. Вычисляем полуширину интервала группировки:
d = (x2*- x1* )/2 =…= (x*m+1- xm* )/2 = (0.27118 - 0.09073)/2 = 0.090225
4.2. Находим xmin = x1*-d = 0.09073-0.090225 = 0.00050500000000002 и xmax = x21*+d = 3.69973+0.090225 = 3.789955
4.3. Находим границы интервалов группировки по формуле xk-1 = xk*-d k = 1…21
| Номер Интервала k | Центр Интервала xk* | Границы Интервала [xk-1 , xk ] | nk*/n | Hk |
| 1 | 0.09073 | 0.00051... 0.18095 | 0.27143 | 1.50418 |
| 2 | 0.27118 | 0.18095... 0.36140 | 0.18214 | 1.00938 |
| 3 | 0.45163 | 0.36140... 0.54185 | 0.13929 | 0.77188 |
| 4 | 0.63208 | 0.54185... 0.72230 | 0.12857 | 0.71250 |
| 5 | 0.81253 | 0.72230... 0.90275 | 0.07500 | 0.41563 |
| 6 | 0.99298 | 0.90275... 1.08320 | 0.06429 | 0.35625 |
| 7 | 1.17343 | 1.08320... 1.26365 | 0.03214 | 0.17813 |
| 8 | 1.35388 | 1.26365... 1.44410 | 0.02500 | 0.13854 |
| 9 | 1.53433 | 1.44410... 1.62455 | 0.02143 | 0.11875 |
| 10 | 1.71478 | 1.62455... 1.80500 | 0.02143 | 0.11875 |
| 11 | 1.89523 | 1.80500... 1.98545 | 0.01429 | 0.07917 |
| 12 | 2.07568 | 1.98545... 2.16590 | 0.00714 | 0.03958 |
| 13 | 2.25613 | 2.16590... 2.34635 | 0.00000 | 0.00000 |
| 14 | 2.43658 | 2.34635... 2.52680 | 0.00357 | 0.01979 |
| 15 | 2.61703 | 2.52680... 2.70725 | 0.00000 | 0.00000 |
| 16 | 2.79748 | 2.70725... 2.88770 | 0.00357 | 0.01979 |
| 17 | 2.97793 | 2.88770... 3.06815 | 0.00357 | 0.01979 |
| 18 | 3.15838 | 3.06815... 3.24860 | 0.00000 | 0.00000 |
| 19 | 3.33883 | 3.24860... 3.42905 | 0.00000 | 0.00000 |
| 20 | 3.51928 | 3.42905... 3.60950 | 0.00000 | 0.00000 |
| 21 | 3.69973 | 3.60950... 3.78995 | 0.00714 | 0.03958 |
4.4. Убеждаемся, что сумма всех высот Hk , умноженная на h, равна единице. (допускается небольшое отличие от единицы в рамках погрешности вычислений)
1.50418+ 1.00938+ ... + 0.03958 = 5.54170 ; 5.54170* 0.18045 = 1.00000
4.5. На оси абсцисс выбираем начальную точку чуть левее точки x1 = 0.18095, и такой масштаб, чтобы на оси поместился интервал [x1 , x21 ] = [ 0.18095 , 3.78995] и отчетливо различались точки xk.
4.6. На оси ординат выбираем начало отсчета в точке 0 и такой масштаб, чтобы отчетливо различались Hk
4.7. Для построения гистограммы относительных частот на ось абсцисс наносим интервалы [xk-1 , xk] и, используя каждый из них как основание, строим прямоугольник с соответствующей высотой Hk.
Получаем гистограмму, изображенную на рисунке ниже.
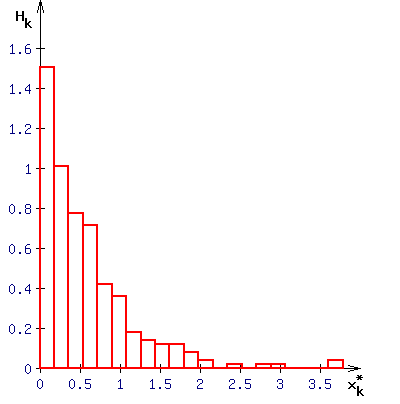
5. Строим эмпирическую функцию распределения.
Эмпирической функцией распределения называется функция F*(x), определенная для всех х от — ∞ до + ∞; таких, что:1) F*(x) = 0, для всех x < x*1;.
2) F*(x) = (n1*/n)+(n2*/n)+…+(nk*/n) для всех x удовлетворяющих условию: хk*≤ x < х*k+1;
3) F*(x) = 1, для всех x ≥ x*m;.
5.1. Для построения функции заполним таблицу (см.ниже), в колонку F*(x) будем записывать накопленные относительные частоты
F*(x1*) = n1*/n
F*(x2*) = (n1*/n)+(n2*/n)
F*(x3*) = (n1*/n)+(n2*/n)+(n3*/n) и т.д.
| Номер Интервала k | Центр Интервала xk* | nk*/n | F*(xk*) |
| 1 | 0.09073 | 0.27143 | 0.27143 |
| 2 | 0.27118 | 0.18214 | 0.45357 |
| 3 | 0.45163 | 0.13929 | 0.59286 |
| 4 | 0.63208 | 0.12857 | 0.72143 |
| 5 | 0.81253 | 0.07500 | 0.79643 |
| 6 | 0.99298 | 0.06429 | 0.86071 |
| 7 | 1.17343 | 0.03214 | 0.89286 |
| 8 | 1.35388 | 0.02500 | 0.91786 |
| 9 | 1.53433 | 0.02143 | 0.93929 |
| 10 | 1.71478 | 0.02143 | 0.96071 |
| 11 | 1.89523 | 0.01429 | 0.97500 |
| 12 | 2.07568 | 0.00714 | 0.98214 |
| 13 | 2.25613 | 0.00000 | 0.98214 |
| 14 | 2.43658 | 0.00357 | 0.98571 |
| 15 | 2.61703 | 0.00000 | 0.98571 |
| 16 | 2.79748 | 0.00357 | 0.98929 |
| 17 | 2.97793 | 0.00357 | 0.99286 |
| 18 | 3.15838 | 0.00000 | 0.99286 |
| 19 | 3.33883 | 0.00000 | 0.99286 |
| 20 | 3.51928 | 0.00000 | 0.99286 |
| 21 | 3.69973 | 0.00714 | 1.00000 |
5.2. На оси абсцисс выбираем начальную точку чуть левее точки x1* = 0.09073, и такой масштаб, чтобы на оси поместился интервал [x1* , x21* ] = [ 0.09073 , 3.69973] и отчетливо различались точки xk*.
5.3. На оси ординат выбираем начало отсчета в точке 0 и такой масштаб, чтобы на оси поместился интервал
[0 , 1] и отчетливо различались точки nk*/n.
5.4. Для построения графика эмпирической функции распределения наносим на ось абсцисс интервалы [xk* , xk+1*] и над каждым из них на высоте F*(xk* ) строим горизонтальные отрезки. В правом конце отрезка помещаем стрелку, чтобы показать, что F*(xk* ) в точке x*k+1 делает прыжок в высоту на F*(x*k+1 ) — F*(xk* ) = n*k+1 /n.
Получаем график эмпирической функции распределения, изображенный на рисунке ниже.
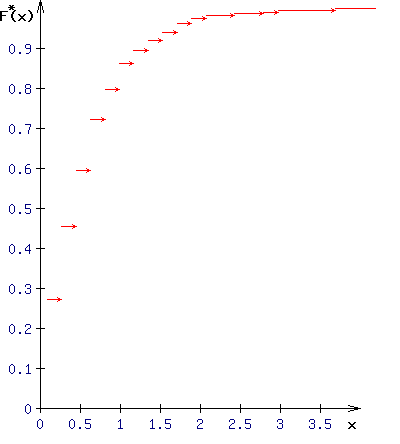
6. Вычислим оценку математического ожидания (выборочное среднее) исходного ряда абсолютных частот.
Выборочное среднее группированного статистического ряда абсолютных частот определяется формулой| M* = |
| xk*(nk*/n) |
Чтобы упростить вычисления и уменьшить погрешность округления, используем так называемый метод произведений. Заметим, что если c — центр того интервала группировки, который находится примерно в середине статистического ряда и h — длина интервала группировки, то величины
| yk* = |
|
| Y* = |
|
| yk*nk* |
M* = Y*h + c (6.1)
Реализовать данный метод удобно с помощью таблицы (см. ниже)
6.1. Вычисляем длину интервала группировки
h = x2*- x1* =…= x*m+1- xm* = 0.27118 - 0.09073 = 0.18045
6.2. Выбираем c = x11* = 1.89523 (середина ряда)
6.3. Заполняем 4-й столбец величинами yk*. В строке с x11* = c пишем 0, вверх записываем последовательно — 1, —2, и т.д., а вниз — последовательно 1, 2, и т.д.
6.4. Заполняем 5-й столбец величинами yk*nk*. Таблица принимает вид
| Номер Интервала k |
Центр Интервала xk* |
nk* | yk* | yk*nk* |
| 1 | 0.09073 | 76 | -10 | -760 |
| 2 | 0.27118 | 51 | -9 | -459 |
| 3 | 0.45163 | 39 | -8 | -312 |
| 4 | 0.63208 | 36 | -7 | -252 |
| 5 | 0.81253 | 21 | -6 | -126 |
| 6 | 0.99298 | 18 | -5 | -90 |
| 7 | 1.17343 | 9 | -4 | -36 |
| 8 | 1.35388 | 7 | -3 | -21 |
| 9 | 1.53433 | 6 | -2 | -12 |
| 10 | 1.71478 | 6 | -1 | -6 |
| 11 | 1.89523 | 4 | 0 | 0 |
| 12 | 2.07568 | 2 | 1 | 2 |
| 13 | 2.25613 | 0 | 2 | 0 |
| 14 | 2.43658 | 1 | 3 | 3 |
| 15 | 2.61703 | 0 | 4 | 0 |
| 16 | 2.79748 | 1 | 5 | 5 |
| 17 | 2.97793 | 1 | 6 | 6 |
| 18 | 3.15838 | 0 | 7 | 0 |
| 19 | 3.33883 | 0 | 8 | 0 |
| 20 | 3.51928 | 0 | 9 | 0 |
| 21 | 3.69973 | 2 | 10 | 20 |
6.5. Суммируем частоты nk* в 3-м столбце и получаем объем выборки = 280.
6.6. Суммируем числа yk*nk*, в 5-м столбце. Получаем -2038.
Делим этот результат на n = 280 и получаем величину Y* = -7.27857.
6.7. По формуле (6.1) вычисляем искомое выборочное среднее:
M* = Y*h + c = -7.27857 •0.18045 + 1.89523 = 0.58181.
ОТВЕТ.
Оценка математического ожидания (выборочное среднее) исходного ряда составляет: 0.581812
7. Вычислим оценку дисперсии (выборочную дисперсию) исходного ряда абсолютных частот.
Оценка дисперсии группированного статистического ряда абсолютных частот определяется формулой| Dx* = |
| = |
|
| (xn*- M* )2nk*, |
Чтобы упростить вычисления и уменьшить погрешность округления, используем так называемый метод произведений.
Заметим, что выборочная дисперсия D* не изменится, если из каждой величины хk* вычесть одно и то же число с. Пусть c — центр того интервала группировки, который находится примерно в середине статистического ряда и h — длина интервала группировки, то величины
| yk* = |
|
| Dy* = |
|
| (yk* - Y*)2 nk* = |
| [n |
| y*2k nk* - ( |
| y*k nk*)2] (7.1) |
Dx* = h2 Dy* (7.2)
Реализовать данный метод удобно с помощью таблицы (см. ниже)
7.1. Вычисляем длину интервала группировки
h = x2*- x1* =…= x*m+1- xm* = 0.27118 - 0.09073 = 0.18045
7.2. Выбираем c = x11* = 1.89523 (середина ряда)
7.3. Заполняем 4-й столбец величинами yk*. В строке с x11* = c пишем 0, вверх записываем последовательно — 1, —2, и т.д., а вниз — последовательно 1, 2, и т.д.
7.4. Заполняем 5-й столбец величинами yk*nk*.
7.5. Заполняем 6-й столбец величинами yk*2. В строке с x11* = c пишем 0, вверх записываем последовательно квадраты натуральных чисел 1, 4, 9, 16, 25 и т.д., и вниз также последовательно 1, 4, 9, 16, 25 и т.д.
7.6. Заполняем 7-й столбец величинами ( yk* )2nk*. Таблица принимает вид
| Номер Интервала k |
Центр Интервала xk* |
nk* | yk* | yk*nk* | yk*2 | yk*2nk* |
| 1 | 0.09073 | 76 | -10 | -760 | 100 | 7600 |
| 2 | 0.27118 | 51 | -9 | -459 | 81 | 4131 |
| 3 | 0.45163 | 39 | -8 | -312 | 64 | 2496 |
| 4 | 0.63208 | 36 | -7 | -252 | 49 | 1764 |
| 5 | 0.81253 | 21 | -6 | -126 | 36 | 756 |
| 6 | 0.99298 | 18 | -5 | -90 | 25 | 450 |
| 7 | 1.17343 | 9 | -4 | -36 | 16 | 144 |
| 8 | 1.35388 | 7 | -3 | -21 | 9 | 63 |
| 9 | 1.53433 | 6 | -2 | -12 | 4 | 24 |
| 10 | 1.71478 | 6 | -1 | -6 | 1 | 6 |
| 11 | 1.89523 | 4 | 0 | 0 | 0 | 0 |
| 12 | 2.07568 | 2 | 1 | 2 | 1 | 2 |
| 13 | 2.25613 | 0 | 2 | 0 | 4 | 0 |
| 14 | 2.43658 | 1 | 3 | 3 | 9 | 9 |
| 15 | 2.61703 | 0 | 4 | 0 | 16 | 0 |
| 16 | 2.79748 | 1 | 5 | 5 | 25 | 25 |
| 17 | 2.97793 | 1 | 6 | 6 | 36 | 36 |
| 18 | 3.15838 | 0 | 7 | 0 | 49 | 0 |
| 19 | 3.33883 | 0 | 8 | 0 | 64 | 0 |
| 20 | 3.51928 | 0 | 9 | 0 | 81 | 0 |
| 21 | 3.69973 | 2 | 10 | 20 | 100 | 200 |
7.5. Суммируем частоты nk* в 3-м столбце и получаем объем выборки = 280.
7.6. Суммируем числа yk*nk*, в 5-м столбце. Получаем -2038.
Возводим это число в квадрат и получаем 4153444.
7.7. Суммируем числа yk*2nk*, в 7-м столбце. Получаем 17706.
7.8. По формуле (7.1) вычисляем D*y:
| D*y = |
|
[280 • 17706 - 4153444] ≈ 10.294880 |
7.9. По формуле (7.2) вычисляем D*x:
Dx* = h2 Dy* = 0.180452 • 10.294880 ≈ 0.335224
ОТВЕТ.
Оценка дисперсии (выборочная дисперсия) исходного ряда составляет: 0.335224
см. пример обработки не сгруппированной выборки...
решить мою задачу...
на ввод условия...
к списку решаемых задач...